在讲算法之前，还是先讲一下几个概念：

什么是算法

算法是在解决特定问题时，给出的步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或者多个步骤

C语言语法简单，强调数据结构，很适合算法和数据结构说明，另外笔者使用cygwin64，安装gcc-core、gcc-g++和make，具体安装方法，请读者自行百度安装。

例如如下代码，笔者使用C/C++语言进行代码编写，

#include <stdio.h>

/**
* 累加到给出的自然数n
* @param [int] n 自然数n
* @return 返回从1到n的自然数之和
*/
int add_to_number(int n)
{

    int sum = 0;
    int i = 0;

    for (i = 1; i <= n; i++)
    {
        sum += i;
    }

    return sum;
}

int main(int args, char *argv)
{
    int n = 100;
    int sum = 0;
    
    sum = add_to_number(n);

    printf("The sum 1 to %d is %d", n, sum);

    return 0;
}

以上简单的一个函数，功能是给出一个自然数n，返回从1累加到n之和，这就是一个算法，函数体中清晰地描述了步骤，计算机根据这些指令进行运算，一直到返回一个和。

编译运行：

$ gcc -o examples/simple.c -o examples/simple

运行结果

算法特性

• 输入和输出

有一个输入或者零个输入，但是必须有输出，这个输出可以是一个简单的打印

例如：

/**
* 简单的调试打印方法
*/
void debug(char *msg)
{
#ifdef DEBUG
	printf("[%s][%d] %s",  __FILE__, __LINE__, msg);
#endif
}

• 有穷性

是指在执行有限的步骤之后，得出一个结果。这个有限的步骤所用的时间可能是毫秒，也可能是几天以后，但是不能无限循环下去，例如咱们平时启动一个web服务，启动之后一直在监听客户端调用。

• 确定性

值得步骤必须是确定的，朝着正确的方向执行，编程都是向着自己可控的方向进行，不能掌控程序的正确性，说明还得练。

• 可行性

算法的每一步都必须是可行的，算法最可恨的应该是数据类型的转换了，一个不小心，Java抛出Null异常，C抛出Segment fault，Python尽管很少报这种异常，但是含有Attr和List的异常出现。

我们在写算法时，一定要先设计好数据结构，必须明确我使用的是什么数据类型，进行什么转换，最后变成什么数据类型，要做到了如指掌，C是基础语言，因此会用C来进行代码撰写和说明。

检验算法的标准

• 正确性

就是输入规定的参数，输出正确的，无歧义的数据，对于输入的参数我们可以进行测试：

• 运行正常无异常产生
• 输入正确，输出正确
• 输入错误，输出错误信息
• 特殊值（精心挑选的数据）输入，无异常输出
• 可读性

一段算法要求有很高的可读性，我们在项目工程上，更需要可读性，在日常的代码维护中很重要，必要的时候需要加上注释，不要出现当时只有我和上帝能懂，一段时间后只有上帝能读懂的情况，，例如：

// 这段算法的意义是什么
++c;
c << 1;

• 健壮性

在编写代码之前要考虑可能出现的异常，也就是在风险管理上，要有风险清单，遇到哪个风险触发对应的风险管理，对于未知的风险，我们可能就要通过测试去进一步完善了，代码健壮性在一步一步地完善之中。

• 速度快和存储低

这里给出时间复杂度大O表示法，记为O(f(n))，其中f(n)是循环变量n的函数，推导大O的方法很简单：

1. 用常数1取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。

举个栗子：

一个算法的时间函数为 f(n) = 1/2 * n^3 + n + 10000

1. f(n) = 1/2 * n^3 + n + 1
2. f(n) = 1/2 *n^3 + 1
3. f(n) = n ^ 3 + 1

最终算法的时间复杂度为O(n^3)，因为1这个常数级复杂度跟n^3来比太微乎极微了，可以省去。

平方阶

int i, j;
for (i = 0; i < n; i++)
{
	for (j = 0; j < n; j++)
  {
  	....
  }
}

时间复杂度为O(n^2)，一般的幂次方函数的表现形式为嵌套多层循环，每次循环都是从1到n。

对数阶

int i = 1;
while(i < n)
{
	i = i * 2;
}

每次循环i 都乘以2，直到x次，到达n，2^x = n，求x就成为log2n，以2为低n的对数。

指数阶

/**
* 斐波那契数列第n项
* @param [int] n 第n项
* @return 返回第n的数
*/
int fab(int n)
{
	if (n == 0 || n == 1)
  {
  	return n
  }
  
  return fab(n-1, n-2)
}

每一项都是由它的后两项确定的，直到递推到n=1或者n=0的时候，才会返回，一分为2，2再分为4，...，也就是2^n。

讨论算法，应该考虑最好情况，最坏情况和平均情况，这是非常重要的。

下面给出时间复杂度对比图，比较直观：

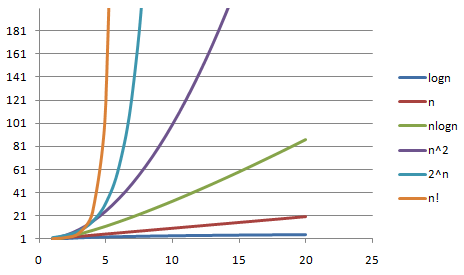
在我们编写算法的过程中，是一个辩证的过程，像哲学中的否定之否定规律，不断的否定我们写过的算法，诞生的新算法更加的符合我们的预期。

算法用到了数学的一些知识，只是达到了应用的层面，后面的算法还会用到矩阵、极限、微积分等，大家不必惊慌，我会举例说明，大家不是考研，不需要研究很深入，但了解背后的数学知识很有必要。